定义:将一个三角形的内部区域填充为特定的颜色、纹理或图案的过程
输入:三角形顶点坐标( x 1 , y 1 ; x 2 , y 2 ; x 3 , y 3 ) (x_1, y_1; x_2, y_2; x_3, y_3) ( x 1 , y 1 ; x 2 , y 2 ; x 3 , y 3 )
输出:三角形内部所有像素点坐标
方法:逐点填充、扫描填充
伪代码实现:
1 2 3 4 5 6 7 8 TriangleRaster (triangle T) { for (int x=0 ;i<xmax;x++) { for (int y=0 ;j<ymax;y++) { if (Inside (T,x,y)) putpixel (x,y); } } }
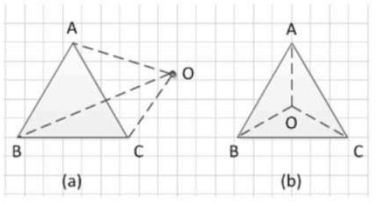
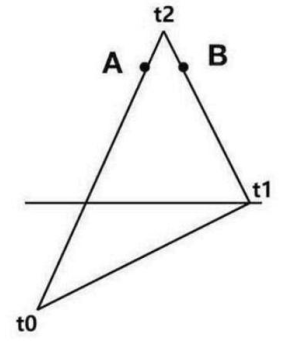
连接点O O O O A OA O A O B OB OB O C OC OC
依次求出S ( A B O ) S(ABO) S ( A BO ) S ( A C O ) S(ACO) S ( A CO ) S ( B C O ) S(BCO) S ( BCO )
如果S ( A B O ) + S ( A C O ) + S ( B C O ) = S ( A B C ) S(ABO)+S(ACO)+S(BCO)=S(ABC) S ( A BO ) + S ( A CO ) + S ( BCO ) = S ( A BC ) O O O
如果S ( A B O ) + S ( A C O ) + S ( B C O ) > S ( A B C ) S(ABO)+S(ACO)+S(BCO)>S(ABC) S ( A BO ) + S ( A CO ) + S ( BCO ) > S ( A BC ) O O O
连接点P P P P A PA P A P B PB PB P C PC PC
求出这三条线段与三角形各边的夹角
如果所有夹角之和为180度,那么点P P P
面积法和内角和法简单直观,但效率低下
如果P在三角形A B C ABC A BC
P,A在BC同侧
P,B在AC同侧
P,C在AB同侧
某一个不满足则说明该点不在三角形内部
将 A P ⃗ \vec{AP} A P A B ⃗ \vec{AB} A B A C ⃗ \vec{AC} A C A B ⃗ \vec{AB} A B 如果P与C在A B AB A B
判断向量同方向可以使用 点积
如果点积大于0, 则两向量夹角是锐角,否则钝角
伪代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 bool PointInTriangle (Vector3 A, Vector3 B, Vector3 C, Vector3 P) return SameSide (A, B, C, P) && SameSide (B, C, A, P) && SameSide (C, A, B, P); } bool SameSide (Vector3 A, Vector3 B, Vector3 C, Vector3 P) Vector3 AB = B - A; Vector3 AC = C - A; Vector3 AP = P - A; Vector3 vl = AB.Cross (AC); Vector3 v2 = AB.Cross (AP); if (vl.Dot (v2) >= 0 ) return true ; else return false ; }
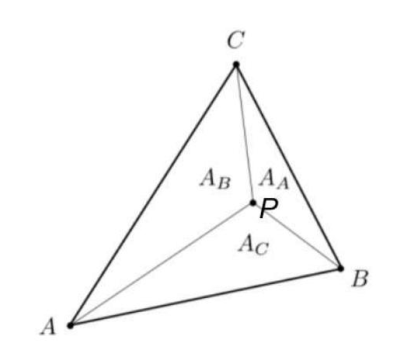
三角形平面中任意点却可以表示为顶点的加权平均值,这些加权称为 重心坐标 (Barycentric Coordinates)
给定三角形A,B,C, 该平面内一点P可以写成这三点的线性组合形式,即 P = α A + β B + γ C P = \alpha A + \beta B + \gamma C P = α A + βB + γ C α + β + γ = 1 \alpha + \beta + \gamma = 1 α + β + γ = 1 ( α , β , γ ) (\alpha, \beta, \gamma) ( α , β , γ )
将一点P与A,B,C三点直接连接, 构成三个三角形面积分别为 A A A_{A} A A A B A_{B} A B A C A_{C} A C α \alpha α β \beta β γ \gamma γ
α = A A A A + A B + A C \alpha = \frac{A_{A} } {A_{A}+A_{B}+A_{C} } α = A A + A B + A C A A β = A B A A + A B + A C \beta = \frac{A_{B} } {A_{A} + A_{B} + A_{C} } β = A A + A B + A C A B γ = A C A A + A B + A C \gamma = \frac{A_{C} } {A_{A} + A_{B} + A_{C} } γ = A A + A B + A C A C
在三角形ABC所在平面中,以A为原点,AB, AC为向量构建坐标系,则P点可写为:
P = A + β ( B − A ) + γ ( C − A ) P = A+\beta(B-A)+\gamma(C-A) P = A + β ( B − A ) + γ ( C − A ) ( 1 − β − γ ) A + β B + γ C (1-\beta-\gamma)A+\beta B+\gamma C ( 1 − β − γ ) A + βB + γ C
定位:
若点P要在三角形内部或边上,需要满足 α > = 0 \alpha>=0 α >= 0 β > = 0 \beta>=0 β >= 0 γ > = 0 \gamma>=0 γ >= 0
插值:
可以根据三个顶点A,B,C的属性插值出任意点的属性,包括位置,颜色,深度,法线向量等P = α A + β B + γ C P = \alpha A + \beta B + \gamma C P = α A + βB + γ C
代数法
[ x B − x A x C − x A y B − y A y C − y A ] [ β γ ] = [ x p − x A y P − y A ] \begin{bmatrix} x_{B}-x_{A}&x_C-x_A\\ y_B-y_A&y_C-y_A\\ \end{bmatrix} \begin{bmatrix}\beta \\ \gamma \end{bmatrix} = \begin{bmatrix} x_p-x_A \\ y_P-y_A\end{bmatrix}
[ x B − x A y B − y A x C − x A y C − y A ] [ β γ ] = [ x p − x A y P − y A ]
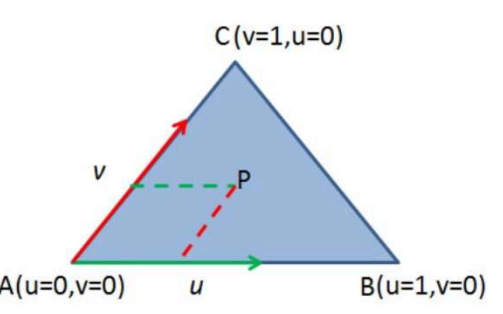
几何法
P = A + u ( B − A ) + v ( C − A ) P=A+u(B-A)+v(C-A)
P = A + u ( B − A ) + v ( C − A )
A − P + u ( B − A ) + v ( C − A ) = 0 A-P+u(B-A)+v(C-A)=0
A − P + u ( B − A ) + v ( C − A ) = 0
u A B ⃗ + v A C ⃗ + P A ⃗ = 0 u\vec{AB}+v\vec{AC}+\vec{PA}=0
u A B + v A C + P A = 0
考虑到坐标有
u A B x ⃗ + v A C x ⃗ + P A x ⃗ = 0 u\vec{AB_x}+v\vec{AC_x}+\vec{PA_x}=0
u A B x + v A C x + P A x = 0
u A B y ⃗ + v A C y ⃗ + P A y ⃗ = 0 u\vec{AB_y}+v\vec{AC_y}+\vec{PA_y}=0
u A B y + v A C y + P A y = 0
写成矩阵形式:
[ u v 1 ] [ A B x ⃗ A C x ⃗ P A x ⃗ ] = 0 \begin{bmatrix} u&v&1 \end{bmatrix} \begin{bmatrix} \vec{AB_x} \\ \vec{AC_x} \\ \vec{PA_x} \end{bmatrix} = 0
[ u v 1 ] A B x A C x P A x = 0
[ u v 1 ] [ A B y ⃗ A C y ⃗ P A y ⃗ ] = 0 \begin{bmatrix} u&v&1 \end{bmatrix} \begin{bmatrix} \vec{AB_y} \\ \vec{AC_y} \\ \vec{PA_y} \end{bmatrix} = 0
[ u v 1 ] A B y A C y P A y = 0
寻找向量( u , v , 1 ) (u,v,1) ( u , v , 1 ) V x ( A B x ⃗ , A C x ⃗ , P A x ⃗ ) V_x(\vec{AB_x},\vec{AC_x},\vec{PA_x}) V x ( A B x , A C x , P A x ) V y ( A B y ⃗ , A C y ⃗ , P A y ⃗ ) V_y(\vec{AB_y},\vec{AC_y},\vec{PA_y}) V y ( A B y , A C y , P A y )
V x = ( B x − A x , C x − A x , A x − P x ) V_x = (B_x-A_x , C_x-A_x , A_x-P_x)
V x = ( B x − A x , C x − A x , A x − P x )
V y = ( B y − A y , C y − A y , A y − P y ) V_y = (B_y-A_y , C_y-A_y , A_y-P_y)
V y = ( B y − A y , C y − A y , A y − P y )
U z = V x × V y U_z=V_x \times V_y
U z = V x × V y
如果U z U_z U z
对于三角形的每一条扫描线,找到对应的左右端点所在区间并进行填充
拆分,把三角形拆成上下两部分
对于上下两部分按下列步骤处理
从y m i n y_{min} y min y m a x y_{max} y ma x
在AB之间填充
利用增量不变可以加速计算,但也使得计算需要按照一定顺序访问像素点,也很难实现并行
扫描填充法如何提高效率?
选择合理的数据结构;
填充多边形、圆、椭圆或其它简单曲线围成的区域多边形光栅化,也称多边形扫描转换
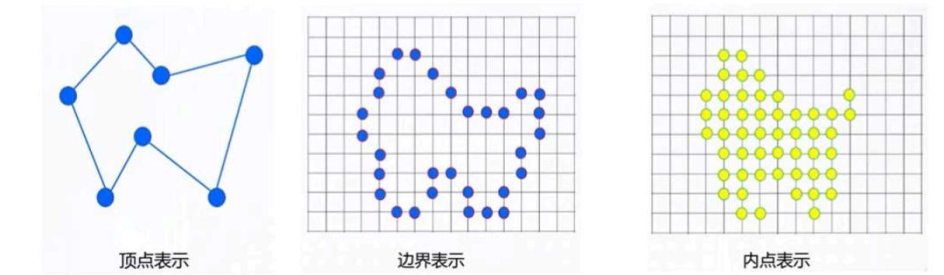
顶点表示 优点:表示直观、几何意义强、占内存少,易于进行几何变换缺点:无法直接用于着色点阵表示 优点:利用多边形边界和内部像素刻画多边形缺点:丢失了许多几何信息
多边形光栅化的基本问题:把多边形的顶点表示转换为点阵表示
和三角形光栅化相似,主要问题是如何判断点是否在多边形内部
算法割断了各像素之间的联系,孤立地考察各像素与多边形的内外关系,使得大量像素都要一一判别
从待判别点P发出射线
若k为奇数,点P位于多边形内
若k为偶数,点P位于多边形外
奇点:射线与多边形边界点的交点为多边形的顶点
极值点:顶点相邻的两边在射线的同侧(2个交点)
非极值点:顶点相邻的两边在射线的异侧(1个交点)
从v点向多边形P顶点发出射线,形成有向角θ i \theta_i θ i
∑ i = 0 n θ i = { 0 , v 位于 P 之外 ± 2 π , v 位于 P 之内 \sum _ {i=0} ^n \theta _i =
\begin{cases}
0, & \text{$v$位于$P$之外} \\
\pm 2\pi, & \text{$v$位于$P$之内}
\end{cases}
i = 0 ∑ n θ i = { 0 , ± 2 π , v 位于 P 之外 v 位于 P 之内
以待测点为圆心作单位圆Σ \Sigma Σ Σ = 0 \Sigma=0 Σ = 0 Σ = 2 π \Sigma=2\pi Σ = 2 π
1 2 3 4 5 6 7 8 9 10 11 void FillPolygonPbyP (Polygon *P, int polygonColor) int x, y; for (y = screen->ymin; y <= screen->ymax; y++) { for (x = screen->xmin; x <= screen->xmax; x++) { if (IsInside (P, x, y)) PutPixel (x, y, polygonColor); else PutPixel (x, y, backgroundColor); } } }
基本思想:按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的像素
确定多边形所占有的最大扫描线数: y min , y max y_{\text{min}}, y_{\text{max}} y min , y max
从y min y_{\text{min}} y min y max y_{\text{max}} y max
当射线与多边形交于某顶点时且该点的两个邻边在射线的上方时,计数0次。下方时,计数2次。两侧时,计数1次。
1 2 3 4 5 6 7 8 9 10 11 12 13 void FillPolygonbySL (Polygon *P, int polygonColor) int y; Edge e; for (y = ymin; y <= ymax; y++) { for (e = first->edge; e <= last->edge; e++) { if (IsIntersect (e, y)) RecordPoint (x, y); SortPoint; 配对; Fill; } } }
算法步骤:假定扫描线是从
y = y min y=y_{\min} y = y m i n 开始向
y = y max y=y_{\max} y = y m a x 的方向移动
初始化ET
初始化AET为空表
AET=ET表中的第一行
从AET中取出交点对进行填充
y i + 1 = y i + 1 y_{i+1}=y_{i}+1 y i + 1 = y i + 1 x i + 1 = x i + 1 / k x_{i+1}=x_{i}+1/k x i + 1 = x i + 1/ k
丢弃旧边:删除y = y max y=y_{\max} y = y m a x
加入新边:合并ET表中y = y i + 1 y=y_{i+1} y = y i + 1
AET不为空则转(4),否则结束
优点:
对每个像素只访问一次
采用增量计算的方法进行交点计算
仅仅在新边加入时排序,且边数远小于扫描线数(<<表示远小于)
缺点:
对各种表的维持和排序开销较大
适合软件实现而不适合硬件实现
计算每一条边与扫描线的交点
逐边向右取补(异或写)
优点:简单
栅栏:一条过多边形顶点且与扫描线垂直的直线
利用栅栏把多边形分为两半
基本思想:按任意顺序处理多边形的每条边,在处理每条边与扫描线的交点间的像素取补
先画边界后填色
用一种特殊的颜色在帧缓冲器中将多边形的边界勾画出来;
将着色的像素点依x坐标递增的顺序两两配对;
将每一对像素所构成的扫描线区间内的所有像素值为填充色;
打标记: 对多边形的每条边进行直线扫描转换(将多边形边界所经过的像素打上标记)
填充:
设置布尔量inside: 内部,真;外部,假
初值:假
遇到标记点:取反
真:填充
假:不填充
算法分析:
边标志算法对每个像素仅访问一次:
利用硬件实现: